ตัวอย่างการคำนวณโครงสร้าง Arch (Design Calculation of Vertical Curve Member)
สำหรับโพสต์นี้ จะเป็นเนื้อหาที่ต่อเนื่องมาจากโพสต์ก่อน เรื่อง Curve Member Design นะครับ ซึ่งเนื้อหาของโพสนี้ หลักๆ ก็จะพูดถึงการออกแบบชิ้นส่วนโครงสร้างที่มีการดัดโค้งในแนวดิ่ง หรือที่เราคุ้นเค้ยกันดีกว่าที่เรียกว่า ARCH นั่นเองครับ ว่าจะต้องมีการพิจารณาพิเศษอะไรเข้ามาเกี่ยวข้องบ้าง เช่น คุณสมบัติของวัสดุที่เปลี่ยนไปเนื่องจากกระบวนการดัด หรือพฤติกรรมทางโครงสร้างที่เปลี่ยนไป
โครงสร้างทรง arch นั้นเป็นรูปแบบของโครงสร้างที่ค่อนข้างจะมีประสิทธิภาพในการรับแรงอัด แต่ในความเป็นจริงแล้วการเกิด pure axial compression นั้นไม่สามารถเกิดขึ้นได้เนื่องจากหลายปัจจัย เช่น imperfection ของ member, การเยื้องศูนย์ รวมถึงแรงกระทำที่ไม่เท่ากันมากระทำพร้อมกันที่ member
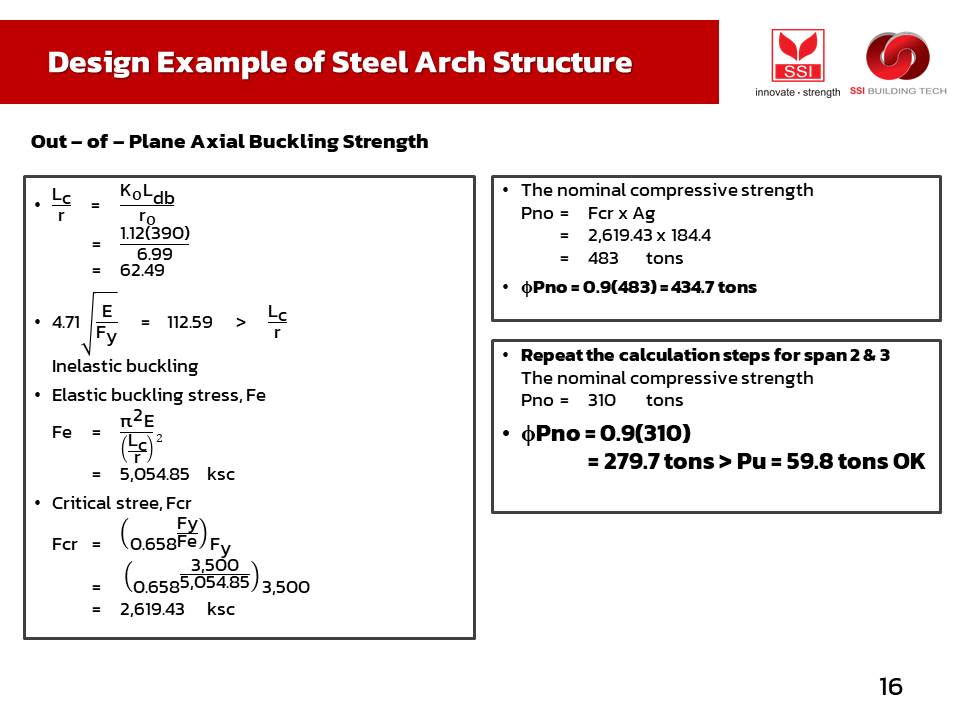
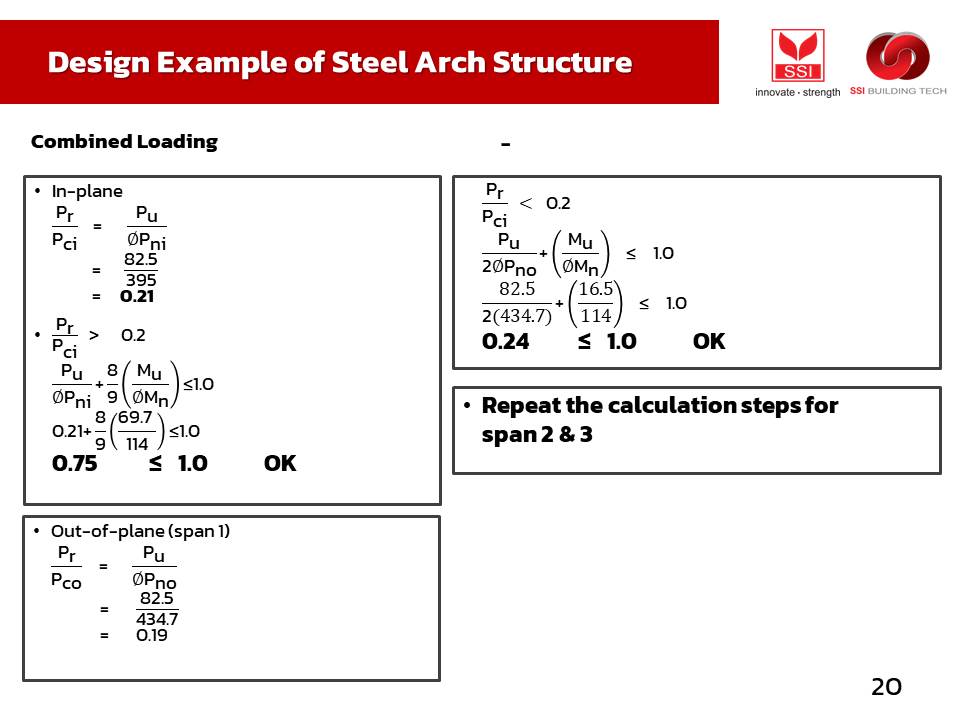
ตัวอย่างการคำนวณอยู่ด้านล่างสุด นะครับ
รูปทรงของ Arch (Geometry)
Funicular shape หรือรูปทรงที่เป็นเหมือนสายไฟฟ้าห้อยๆ ในรูปที่ 2 จะเป็นรูปทรงที่จะสามารถเกิดได้กับ member ที่ต้องรับแรงในแนวแกน (axial loads) และจะเกิดขึ้นเมื่อ load ที่มากระทำมีลักษณะเฉพาะด้วย ซึ่งหากดูรูปที่ 2-a จะเห็นว่าเป็น tension member ที่มีลักษณะเหมือนกัน cable ที่มี load มากระทำ (เหมือนตอนที่เราเรียนฟิสิกส์)
ในทางกลับกัน ถ้าเปลี่ยนการดัดให้เป็นเหมือนคานหน้าบึ้ง รูปที่ 2-b และเอา load มากระทำในลักษณะเดิม ก็จะทำให้รูปแบบของ reaction ที่เกิดขึ้นแตกต่างกัน อีกทั้งยังทำให้เกิดรูปทรงของ moment diagram ที่เหมือนกับคานธรรมดาที่ไม่ได้มีการดัดโค้งอีกด้วย ซึ่งด้วยการที่ load เป็นแบบจุด (concentrated load) จึงทำให้ระบบของโครงสร้างนั้นไม่เกิดการโค้งแบบ arch ซึ่งจะแตกต่างจากการที่ load ที่มากระทำนั้นเป็นแบบ uniform load (รูปที่ 2-c)
สำหรับการคำนวณหา moment และ shear ที่จุดใดๆ บนโครงสร้างประเภทนี้ สามารถทำได้โดยการใช้ประโยชน์จะเส้น offset ที่เกิดจากเส้นโค้งทั้ง 2 (รูปที่ 3) ซึ่งหากวาดออกมาแล้ว เราก็จะได้รูปที่เป็น member ของเรา และอีกเส้นนึงคือ เส้น funicular polygon ที่เกิดจาก load มากระทำ
จุดที่ member ตัดกับเส้น funicular polygon นี้ จะมีค่า bending moment เท่ากับ 0 …. ส่วนในตำแหน่งอื่นๆ บน arch member นั้น ค่า bending moment จะสามารถคำนวณได้จาก axial load คูณกับระยะ offset ที่เกิดขึ้นครับ ดังรูปด้านล่าง
สำหรับโครงสร้างทรง arch แล้ว จะใช้คำว่า rise-to-span ratio H / Ls เป็นตัวกำหนดหน้าตาที่เกิดขึ้น (รูปที่ 4) โดยที่
- H คือ จุดที่ยกตัวสูงสุดของ arch หรือ apex (ถ้าในรูปก็คือ ณ ตำแหน่งกึ่งกลาง)
- Ls คือ ความยาวของ span
ซึ่งค่า rise-to-span ratio ที่จะทำให้เกิดความคุ้มค่าด้านโครงสร้างมากที่สุดจะอยู่ที่ 1/6 และ 1/5
แรงอัดในแนวแกน (Axial Compression)
อย่างที่ได้กล่าวไปก่อนหน้านี้ โครงสร้างทรง arch นั้นจะรับแรงอัดในแนวแกนเป็นหลัก แต่ไม่ได้เกิดแรงอัดอย่างเดียวเหมือน truss นะครับ เนื่องจากมันเกิด bending moment ด้วย ซึ่งการคำนวณก็จะเหมือนกับ combined axial bending member เลย ที่จะต้องคำนวณแรงภายในทั้ง 2 ที่เกิดขึ้นแยกกัน
สำหรับ member ที่เป็นทรง circular arch (รูปที่ 4-a) แรงอัดที่เกิดขึ้น (axial compression load) สามารถคำนวณได้จาก
- Pr = qR โดยที่ R คือรัศมี และ q คือ uniform load ที่กระทำ หน่วยเป็น kg/m.
แต่หาก member มีลักษณะที่เป็นทรง parabolic curve ที่มี uniform load มากระทำ อันนี้สมการก็จะยาวๆ หน่อยครับ ซึ่งมีตัวแปร rise-to-span ratio เข้ามาเกี่ยวข้องด้วย (รูปที่ 5)
การพิจารณา in-plane deflection นั้น ก็จะมีพฤติกรรมเหมือนกับ beam-column member (หรือ combined axial bending member) ครับ อีกทั้งยังต้องมีการพิจารณา second-order effect ร่วมด้วย เนื่องจากรูปทรงของ member นั้นมีลักษณะที่เป็น non-linear (ก็คือ ไม่ตรงนั้นเองครับ) สมการ second-order deflection ในรูป
กำลังรับน้ำหนักรอบแกนหลัก (In-Plane Strength)
ด้วยความที่ โครงสร้างประเภทนี้ จะต้องรับแรงอัดในแนวแกนเป็นหลัก ดังนั้นแล้ว บริเวณ support จึงมีโอกาสที่จะถูกดันออกจนเกิดการเสียรูป (แบะออก ดังรูปที่ 6-a) ซึ่งทำให้กำลังรับน้ำหนักลดลงอย่างมีนัยยะ จนนำไปสู่การพังทลายของโครงสร้างได้ ซึ่งเราเรียกพฤติกรรมนี้ว่า flexible support
แต่การจะทำให้ support นั้นมีความ rigid โดยสมบูรณ์ ก็ทำได้ยากครับ ดังนั้นจึงต้องมีการติดตั้ง member เพิ่มเติม เพื่อเข้ามาช่วยเพิ่ม stiffness ให้กับ support ดังเช่นรูปที่ 6-b ที่นำ member มาติดตั้งเพิ่มในแนวนอนหรือคล้ายๆ กับ strut ซึ่ง member นี้ก็จะทำหน้าเป็น tension tie โดยการรั้ง support ไม่ให้เกิดการแบะออกนั่งเองครับ …. หรืออาจเพิ่ม stiffness ให้กับ support โดยการทำเสาเป็น vertical truss แทน ก็เป็นอีกวิธีหนึ่งที่สามารถช่วยได้เช่นกัน ซึ่งก็ออกแบบ vertical truss ที่รองรับ arch roof เช่นในรูป 6-c ที่แสดง ก็ออกแบบเหมือนกับคานครับ
นอกจากนี้ arch จะต้องถูกออกแบบให้มีเสถียรภาพ หรือกล่าวคือ ไม่ให้เกิดการวิบัติที่เกิดจากการโก่งเดาะ ประเภทที่เรียกว่า snap through buckling ซึ่งเป็นการเสียเสถียรภาพของหน้าตัดในระนาบ สามารถเกิดได้กับหน้าตัดประเภทนี้ ที่เป็นแบบสมมาตรและไม่สมมาตร (รูปที่ 7-a แบบ c คือ การโก่งเดาะของหน้าตัดที่สมมาตร และ b คือ การโก่งเดาะของหน้าตัดที่ไม่สมมาตร)
ซึ่งเราสามารถออกแบบเพื่อป้องกันการโก่งเดาะดังกล่าว (snap through buckling) ได้โดยการจำกัด span slenderness หรือความยาวช่วงของ arch ไม่ให้เกินค่า Ls / ri โดย Ls คือ ความยาวของ span และ ri คือ รัศมีไจเรชั่นของ arch ….. แต่เมื่อป้องกันการเกิด snap through buckling ได้แล้ว ปัญหาต่อมาก็คือ arch จะเกิดการโก่งเดาะในรูปแบบอื่นตามมานั่นเองครับ ดังแสดงในรูปที่ 7-b และ 7-c
กำลังรับน้ำหนักรอบแกนรอง (Out-of-Plane Strength)
แน่นอนครับว่ามี in-plane buckling แล้ว ก็ต้องมี out-of-plane buckling ตามมา สำหรับ compression member ซึ่งในทางปฏิบัตินั้น การจะป้องกันไม่ให้เกิด out-of-plane buckling ก็สามารถทำได้โดยการติดตั้งค้ำยันในแกนอ่อนนั่นเองครับ (รูปที่ 8) …. แต่อย่างไรก็ตาม หากการค้ำยันเป็นการค้ำยันแบบทำเป็นช่วงๆ (discrete braces) การโก่งเดาะก็อาจยังสามารถเกิดขึ้นได้กับ member ที่อยู่ระหว่างจัดที่ทำการค้ำยัน ซึ่งเราสามารถคำนวณหากำลังรับน้ำหนักได้จากสมการ Euler เหมือน AISC Chapter E แต่จะมีความซับซ้อนของสมการเพิ่มขึ้นมา ตามรูป 8
การพิจารณาอื่นๆ ที่เกี่ยวข้อง
นอกจากการพิจารณาที่กล่าวมาข้างต้น ก็ยังมีสิ่งที่ต้องพิจารณาอีกมากมายเลยนะครับ หากต้องการจะออกแบบโครงสร้างลักษณะนนี้ เช่น
- Second-order effect ที่ไปขยายค่าของ bending moment
- Lateral torsional buckling ที่เกิดจากดัดตัวของโครงสร้าง
- การพิจารณา combined axial and flexure loads ที่กระทำกับตัวโครงสร้าง
- Local bending ที่เกิดบริเวณ flange และ local buckling ที่เกิดบริเวณ web
- Web bend buckling ที่อาจเกิดกับ member ที่มีรัศมีน้อยๆ (cold bend เยอะๆ) และ web บางๆ
ซึ่งแน่นอนครับว่า เราจะต้องพิจารณาออกแบบในทุกกรณีที่กล่าวมา เพื่อให้มั่นใจว่า member ของเรานั้นจะไม่เกิดการวิบัติเนื่องจาก limit state อันใดอันหนึ่ง
หวังว่าทุกท่านน่าจะได้รับประโยชน์กันไม่มากก็น้อย